Math Mastery: Mensuration Formulas for 2D and 3D Shapes, PDF Access

Mensuration Formulas: The study of geometric figures and their measurements falls within the field of mensuration in mathematics. It deals with dimensions such as area, surface area, volume, length, and shape, among others.  Measuring geometrical forms that fall into the 2D and 3D shape categories is the main focus of measurement. 

Mensuration Formula in Maths

You can determine and compute the areas, perimeters, volumes, total surface areas, curved surface areas, lengths, and other geometrical numbers with the use of the mensuration formulas. Let's first examine the distinctions between 2D and 3D figures before going on to the mensuration formulas. This essay is crucial not only for kids enrolled in school but also for applicants getting ready for competitive tests where mensuration is a major factor. If you're preparing for the SSC, Bank examinations, or other government examinations, you may be aware that the Quantitative Aptitude section of the papers for the Delhi Police Constable, SSC CGL, SSC CHSL, SSC MTS, SSC CPO, and Bank Exams include topics related to mensuration. These questions typically range from two to three. These formulas for mensuration are also crucial for kids in Classes 8, 9, and 10, so pay attention and let us help you succeed on your tests.

Mensuration Formulas

Even though you may already grasp the differences between 2-D and 3-D shapes, we will split the mensuration formula tables for both shapes below for your convenience. Take a look at the 2-D and 3-D Mensuration Formulas below.

Mensuration Formulas for 2-D Figures

For 2-D figures, the perimeter and area are always computed in units and square units, respectively. You may find a comprehensive list of the areas and perimeters of many 2-D forms, including squares, trapeziums, parallelograms, rhombuses, circles, and triangles (scalene, isosceles, equilateral, and right), in the table below. Examine these mensuration formulas, make sure you comprehend them and commit them to memory.

Mensuration Formulas for 2-Dimensional Figures
Shape	Area	Perimeter
Circle	πr²	2 π r
Square	(side)²	4 × side
Rectangle	length × breadth	2 (length + breadth)
Scalene Triangle	√[s(s−a)(s−b)(s−c), Where, s = (a+b+c)/2	a+b+c (sum of sides)
Isosceles Triangle	½ × base × height	2a + b (sum of sides)
Equilateral Triangle	(√3/4) × (side)²	3 × side
Right Angled Triangle	½ × base × hypotenuse	A + B + hypotenuse, where the hypotenuse is √A²+B²
Parallelogram	base × height	2(l+b)
Rhombus	½ × diagonal1 × diagonal2	4 × side
Trapezium	½ h(sum of parallel sides)	a+b+c+d (sum of all sides)

Mensuration Formulas for 3-D Figures

We may compute the total surface area under 3-D figures, which is equal to the sum of the areas of the top and bottom and the curved surface area. Measured in square units, curved surface area is often referred to as lateral surface area. While volume is measured in cubic units, total surface area is also measured in square units. Thus, learn the mensuration formulas for 3-dimensional forms like spheres, cones, cylinders, cubes, and cuboid shapes.

Mensuration Formulas for 3-Dimensional Figures
Shape	Area	Curved Surface Area (CSA)/  Lateral Surface Area (LSA)	Total Surface Area (TSA)
Cone	(1/3) π r² h	π r l	πr (r + l)
Cube	(side)³	4 (side)²	6 (side)²
Cuboid	length × breadth × height	2 height (length + breadth)	2 (lb +bh +hl)
Cylinder	π r² h	2π r h	2πrh + 2πr²
Hemisphere	(2/3) π r³	2 π r²	3 π r²
Sphere	4/3πr³	4πr²	4πr²

Differences between 2-dimensional and 3-dimensional Figures

Geometry has two different kinds of figures: two-dimensional and three-dimensional figures. To learn about and comprehend the distinctions between 2- and 3-dimensional figures, refer to the table below.

2-Dimensional Figures	3-Dimensional Figures
As the name suggests, a 2D shape means that it will have only 2 dimensions which are length and breadth.	Here, a 3D shape means that this figure will have 3 dimensions, which are length, breadth, and height.
For 2D shapes, we can calculate 2 things i.e. area and perimeter.	For 3D shapes, we can calculate their volume, total surface area, and curved/lateral surface area.
2D shapes are flat as they do not have depth and also, these cannot be held physically because of the lack of depth.	3D shapes contain a depth so they can be held physically and are not flat like 2D shapes.
Example: Square, Rectangle, Triangle, Circle, etc.	Example: Cone, Cylinder, Sphere, Cube, Prism, Pyramid, etc.

Mensuration Formulas PDF

Download the PDF from the link below to gain a thorough understanding of the mensuration formulas for each 2- and 3-dimensional figure. Then, effectively practice the problems. Using the links provided below, you can also download the Mensuration Formulas PDF.

Mensuration Formulas PDF 1- Click to Download

Mensuration Formulas PDF 1- Click to Download

Mensuration Formulas Examples

Mensuration maths formulas for all 2-D and 3-D figures are discussed below in detail.

1. Cube Formula

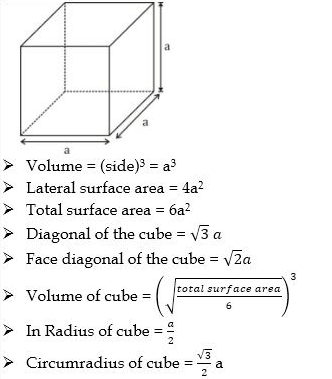
2. Cuboid Formula

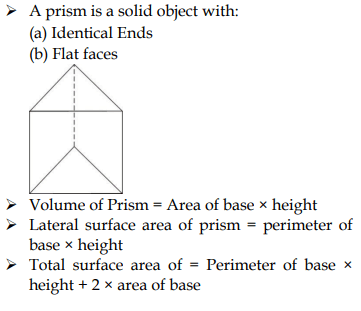
3. Prism Formula

4. Sphere Formula

5. Hemisphere Formula

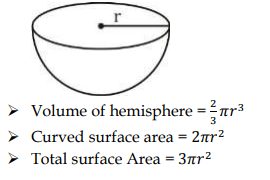
6. Pyramids Formula

7. Right Circular Cone Formula

8. Right Circular Cylinder Formula

Important Terms Related to Mensuration Formula

Before we get into the formulas for mensuration, let's understand some important terms:

• Perimeter: This is the measure of the continuous length around the boundary of a shape, and it's measured in units like meters (m) or centimeters (cm).
• Area: It is the surface enclosed within a shape and is measured in square units like square meters (m²) or square centimeters (cm²).
• Volume: This measures the space occupied by an object and is expressed in cubic units such as cubic meters (m³) or cubic centimeters (cm³).
• Curved/Lateral Surface Area: This is the measurement of the curved surface in a shape and is expressed in square units like square meters (m²) or square centimeters (cm²).
• Total Surface Area: This represents the overall surface area of a shape, including the top and bottom portions, and is measured in square units like square meters (m²) or square centimeters (cm²).

Mensuration Questions with Solutions

Q1. Find the area of a rhombus whose diagonals are of lengths 9 cm and 7.2 cm. 

Solution: Now, d1=9 cm, d2=7.2 cm where d1 and d2 are the lengths of diagonals of a rhombus.

Area of rhombus formula is ½ (d1xd2) 

Therefore, area of the given rhombus = ½ x 9 x 7.2 cm² = 32.4 cm²

Note: Here, the value of π is either considered as 22/7 or 3.14, r means radius, and h means height.

Q2. A rectangular paper of a width of 10 cm is rolled along its width and a cylinder of a radius of 18 cm is formed. Find the volume of the cylinder. (Take π=22/7)

Solution: A cylinder is formed by rolling a rectangle of 10 cm about its width. The radius of the cylinder is 18 cm and the width of the paper becomes the height.

Height of the cylinder, h = 10 cm and Radius of the cylinder, r = 18 cm

Now, volume of the cylinder, V = πr²h = (22/7) x (18)² x 10

= 10,183 cm³

Hence, the volume of the cylinder is 10183 cm³.

Q3. A circle has a radius of 21 cm. Find its circumference and area. (Use π = 22/7)

Solution: We know, Circumference of circle = 2πr = 2 x (22/7) x 21 = 2 x 22 x 3 = 132 cm

Area of circle = πr² = (22/7) x (21)² = 22/7 x 21 x 21 = 22 x 3 x 21

Area of a circle with a radius, of 21cm = 1386 cm²

Q4. The length, width, and height of a cuboidal box are 30 cm, 25 cm, and 20 cm, respectively. Find its area.

Solution: Here, l- 30 cm, b= 25 cm, and h= 20 cm

Total surface area = 2 (lb +bh +hl)

= 2 (30 × 25 + 25 × 20 + 20 × 35)

TSA = 2( 750 + 500 + 700) = 3900 cm²

Q5. A rectangular piece of paper 11 cm × 4 cm is folded without overlapping to make a cylinder of the height of 4 cm. Find the volume of the cylinder.

Solution: The length of the paper will be the perimeter of the base of the cylinder and the width will be its height.

Circumference of base of cylinder = 2πr = 11 cm

2 x 22/7 x r = 11 cm

r = 7/4 cm

Volume of cylinder = πr²h = (22/7) x (7/4)² x 4 = 38.5 cm³

Q6. The tangents drawn at points A and B of a circle with Centre O, meet at P. If ∠AOB = 120° and AP= 6cm, then what is the area of triangle (in cm²) APB?

Solution: 

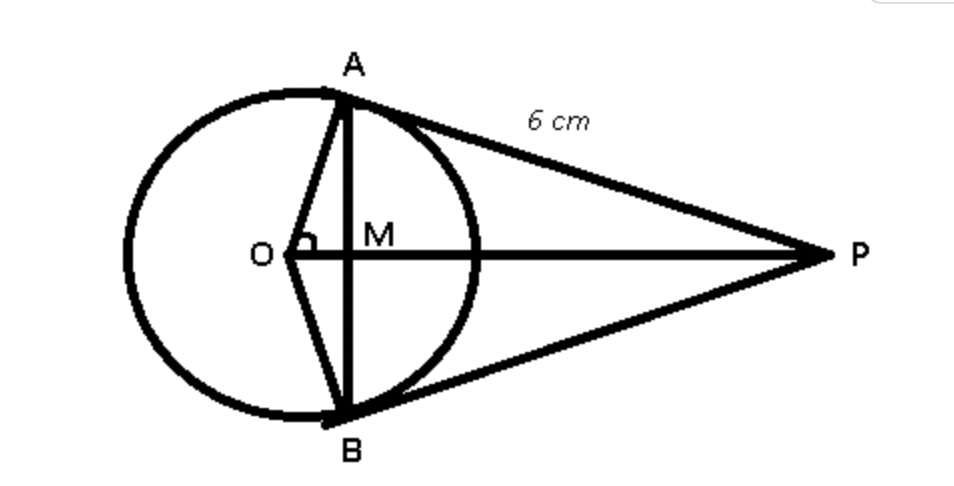
Given ∠AOB = 120° and AP= 6cm and ∠OAP = 90°

∠AOP= ½∠AOB = 120/2 = 60°

In △AOP, >tan (∠AOP) = AP/OA

=> tan 60° = 6/OA

=> √3 = 6/OA

=> OA = 6/√3  = 2√3 cm

Thus, area of △AOP = ½ x (OA) x (AP)

=> ½ x (2√3) x (6) = 6√3 cm² ……………….. (i)

Now, in △AOM

=> sin(∠AOM) = AM/OA

=> sin 60° = AM/2√3

=> √3/2 = AM/2√3

=> AM = 3 cm

Similarly OM= √3 cm

Thus, area of △AOM = ½ x (OM) x (AM)

=> ½ x (√3) x (3) = 1.5√3 cm² ……………….. (ii)

Now, ar(△AMP) = ar(△AOP) - ar(△AOM)

=> 6√3 -1.5√3  = 4.5 √3 cm²

∴ ar(△APB) = 2ar(△AMP) 

= 2 x 4.5√3 = 9√3 cm²

Q7. The total surface area of a hemisphere is 166.32 cm², find its curved surface area?

Solution:  Let radio of hemisphere = r cm 

Total surface area of hemisphere = 3 π r² = 166.32 ……………….. (i)

Multiplying equation (i) by ⅔

=> ⅔ x 3 π r² = ⅔ x 166.32

=> Curved surface area of hemisphere = 2 π r² = 2 x 55.44 = 110.88 cm²

Q8. If G is the centroid and AD, BE, and CF are three medians of the triangle with 72 cm², then the area of triangle BDG is: 

Solution: The area of the triangle formed by any two vertices and centroid is ⅓) times the area of △ABC. 

Also, the median divides the triangle into two equal areas. 

So, the area of △BDG = 1/6 times of △ABC

=> 1/6 x 72

=> 12

Q9. The perimeters of two similar triangles ABC and PQR are 156 cm and 46.8 cm respectively. If BC= 19.5 cm and QR= x cm, then the value of x is?

Solution: (△ABC) Perimeter/ (△PQR) Perimeter) = BC/QR

=> 15.6/46.8 = 19.5/x

=> x = 46.8 x 19.5 / 156 

=> 5.85 cm

Q10. A solid metallic sphere of radius 10 cm is melted and recast into spheres of radius 2 cm each. How many such spheres can be made?

Solution: As, V = 4/3 π r³ 

The volume of the big sphere = n x volume of a small sphere

=> 4/3 π (10)³ = n x 4/3 π (2)³ 

=> n = 125

Conclusion

Mensuration is a wide and practical issue, making it both an interesting and challenging topic to cover. Additionally, a lot of formulas are present, which some students find challenging to remember. Well, if you practice a few questions on the subject on a daily basis and review all the formulas, this should be simple. We hope you will find our Mensuration Formulas essay to be useful and instructive. Keep checking back for more articles like this one.